Exercises
Submission
To submit your solutions create a folder called lab4 and push one or more files to your repository with your answers.
Individual
Please push the deliverables into your personal repository, for math-related questions PDFs typeset with LaTeX or other word processing software are required.
Team
Deadline
Deadline: the VNAV staff will clone your repository on October 4th at 1 PM ET.
👤 Individual
📨 Deliverable 1 - Single-segment trajectory optimization (20 pts)
Consider the following minimum velocity ($r=1$) single-segment trajectory optimization problem:
\[\begin{eqnarray} \min_{P(t)} \quad \int_0^1 (P^{(1)}(t))^2 dt, \label{eq:minvel} \\\ s.t. \quad P(0) = 0, \label{eq:initpos} \\\ \quad P(1) = 1, \label{eq:finalpos} \end{eqnarray}\]with $P(t) \in \mathbb{R}[t]$, i.e., $P(t)$ is a polynomial function in $t$ with real coefficients:
\begin{equation} P(t) = p_N t^N + p_{N-1} t^{N-1} + \dots + p_1 t + p_0. \end{equation}
Note that because of constraint (\ref{eq:initpos}), we have $P(0)=p_0=0$, and we can parametrize $P(t)$ without a scalar part $p_0$.
1. Suppose we restrict $P(t) = p_1 t$ to be a polynomial of degree 1, what is the optimal solution of problem (\ref{eq:minvel})? What is the value of the cost function at the optimal solution?
2. Suppose now we allow $P(t)$ to have degree 2, i.e., $P(t) = p_2t^2 + p_1 t$.
(a) Write $\int_0^1 (P^{(1)}(t))^2 dt$, the cost function of problem (\ref{eq:minvel}), as $\boldsymbol{p}^T \boldsymbol{Q} \boldsymbol{p}$, where $\boldsymbol{p} = [p_1,p_2]^T$ and $\boldsymbol{Q} \in \mathcal{S}^2$ is a symmetric $2\times 2$ matrix.
(b) Write $P(1) = 1$, constraint (\ref{eq:finalpos}), as $\boldsymbol{A}\boldsymbol{p} = \boldsymbol{b}$, where $\boldsymbol{A} \in \mathbb{R}^{1 \times 2}$ and $\boldsymbol{b} \in \mathbb{R}$.
(c) Solve the Quadratic Program (QP): \begin{equation} \min_{\boldsymbol{p}} \boldsymbol{p}^T \boldsymbol{Q} \boldsymbol{p} \quad s.t. \quad \boldsymbol{A} \boldsymbol{p} = \boldsymbol{b}. \label{eq:QPtrajOpt} \end{equation} You can solve it by hand, or you can solve it using numerical QP solvers (e.g., you can easily use the quadprog function in Matlab). What is the optimal solution you get for $P(t)$, and what is the value of the cost function at the optimal solution? Are you able to get a lower cost by allowing $P(t)$ to have degree 2?
3. Now suppose we allow $P(t) = p_3t^3 + p_2 t^2 + p_1 t$:
(a) Let $\boldsymbol{p} = [p_1,p_2,p_3]^T$, write down $\boldsymbol{Q} \in \mathcal{S}^3, \boldsymbol{A} \in \mathbb{R}^{1\times 3}, \boldsymbol{b} \in \mathbb{R}$ for the QP (\ref{eq:QPtrajOpt}).
(b) Solve the QP, what optimal solution do you get? Do this example agree with the result we learned from Euler-Lagrange equation in class?
4. Now suppose we are interested in adding one more constraint to problem (\ref{eq:minvel}):
\begin{eqnarray} \min_{P(t)} \quad \int_0^1 (P^{(1)}(t))^2 dt, \label{eq:minveladd} \
s.t. \quad P(0) = 0, \
\quad P(1) = 1, \
\quad P^{(1)}(1) = -2. \end{eqnarray} Using the QP method above, find the optimal solution and optimal cost of problem (\ref{eq:minveladd}) in the case of:
(a) $P(t) = p_2t^2 + p_1 t$, and
(b) $P(t) = p_3t^3 + p_2 t^2 + p_1t$.
📨 Deliverable 2 - Multi-segment trajectory optimization (15 pts)
1. Assume our goal is to compute the minimum snap trajectory ($r= 4$) over $k$ segments. How many and which type of constraints (at the intermediate points and at the start and end of the trajectory) do we need in order to solve this problem? Specify the number of waypoint constraints, free derivative constraints and fixed derivative constraints.
- Hint: According to Euler-Lagrange method, what is the degree of the polynomial of each segment?
- Hint: How many unknown parameters do we need to solve?
- Hint: How many constraints does each waypoint/free derivative/fixed derivative constraint provide?
- Hint: See figure for $k=3$ as described in the lecture notes.
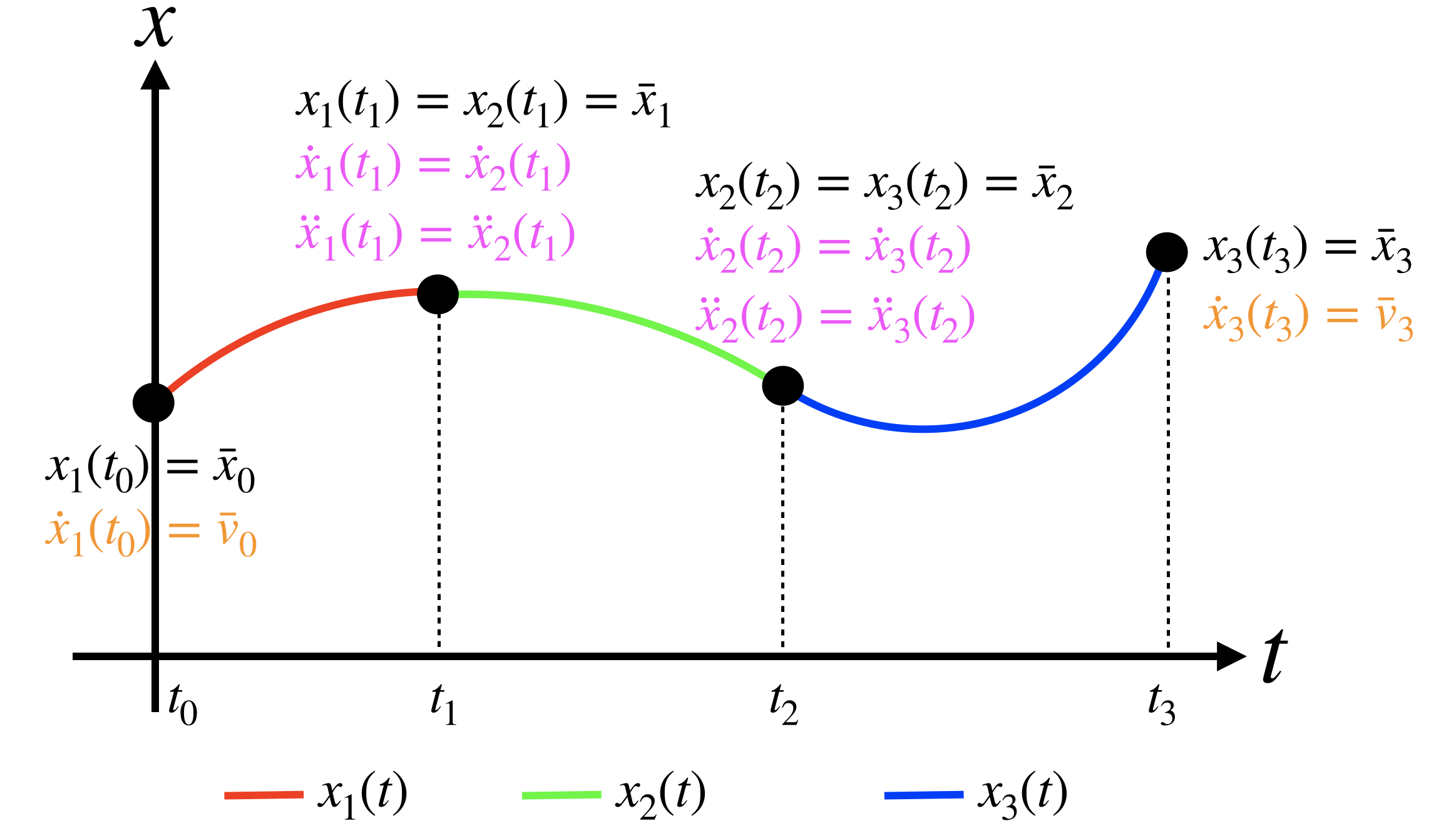
2. Can you extend the previous question to the case in which the cost functional minimizes the $r$-th derivative and we have $k$ segments?
👥 Team
📨 Deliverable 3 - Drone Racing (65 pts)
For this lab we will be racing our simulated our simulated quadcopters in a drone racing course we prepared in our Unity simulator!
- Implement all the missing parts in the code (labeled as Part 0, Part 1.1, Part 1.2, and Part 1.3, see below)
- A video showing the quadrotor completing the race course. Please upload the video onto either Google drive or Dropbox, generate a publicly viewable link, and put the link in a text file called
rviz_drone_race.txtin your repo. - A rosbag of your complete and fastest run. Upload the rosbag onto either Google drive or Dropbox, generate a publicly viewable link, and put the link also in
rviz_drone_race.txt. To record the rosbag,rosbag record /current_state /desired_state
Getting the codebase
First, let’s set up our workspace:
# change the folder name according to your setup
cd ~/labs
git pull
In ~/labs/lab4 we now have the planner_pkg, trajectory_generation_pkg, and dependencies folders, the first two are ROS packages that you will be modifying for this lab, and dependencies should contain all the dependencies you need for this lab.
cp -r ~/labs/lab4/. ~/vnav_ws/src
cd ~/vnav_ws
mav_comm
If you still have the cloned mav_comm repo in your workspace, remove it as the dependencies folder contain a copy of mav_comm as well.
In your src folder, you should see the folders: controller_pkg, tesse-ros-bridge, planner_pkg, trajectory_generation_pkg, and dependencies. The controller_pkg should be your team’s implementation from Lab 3. Now, compile the new code.
catkin build
source devel/setup.bash
After doing so, please proceed here to download the new binary executable for the simulator we are going to use for lab 4. Unzip the file, put the folder in ~/vnav-builds, and run the following commands:
cd ~/vnav-builds/lab4/
chmod +x lab4.x86_64
Try launch the simulator, the simulator should look like this 
Also, the launch files provided in the lab4 folder do not contain the tuned gain values from lab 3. You need to copy the controller gains ROS parameters in the traj_tracking.launch file to the traj_following.launch and static_point_test.launch file in trajectory_generation_pkg.
Controller gains
It's possible that you may need to adjust your controller gains from lab 3 to achieve good performance in lab 4.
Before you start coding, keep in mind that the system we are aiming for is as follows. Pieces are coming together and we are getting closer and closer to the full system that we have seen so often in class! 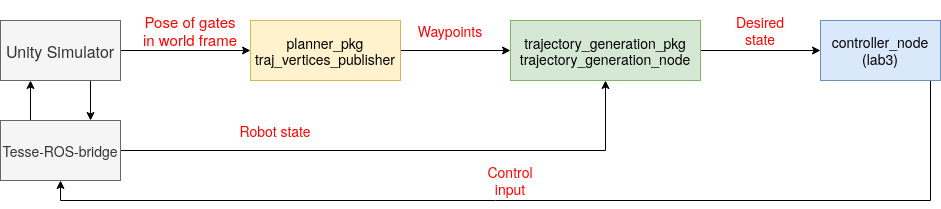
Journey of a thousand miles starts with a single step
As a warm up exercise, let’s just fly and hover at the first gate! Follow the instructions for Part 0 inside planner_pkg/src/simple_traj_planner.cpp
Now fire up the simulator and test. In one terminal window, run
cd ~/vnav-builds/lab4/
./lab4.x86_64
In another terminal, launch tesse_ros_bridge to connect ROS to the simulator,
roslaunch tesse_ros_bridge tesse_quadrotor_bridge.launch
Finally launch the test to hover at the first gate
roslaunch planner_pkg static_point_test.launch
- Hint: you can press
rto respawn your quadcopter - Hint: review the handout from lab 3 if you have trouble running the simulator.
Waypoint publishing
We have already written this node for you in planner_pkg/src/traj_vertices_publisher.cpp. What we are doing here is reading the position and orientation of the gates in the racing course and publishing them as waypoints for trajectory optimization. The topic to note here is /desired_traj_vertices, which should contain a geometry_msgs::PoseArray type storing the position and orientation of the gates on the racing course.
Trajectory generation and following
Follow the instructions for Part 1 in trajectory_generation_pkg/src/trajectory_generation_node.cpp to get your quadcopter ready for drone racing! This node will subscribe to the waypoints published and use them for trajectory optimization using the mav_trajectory_generation library, and then based on the trajectory, publish the desired state at time t to your controller.
- Hint: use
vertex.addConstraint(POSITION, position)where position is of typeEigen::Vector3dto enforce a waypoint position. - Hint: use
vertex.addConstraint(ORIENTATION, yaw)where yaw is a double to enforce a waypoint yaw. - Hint: remember angle wraps around 2$\pi$. Be careful!
- Hint: for the ending waypoint for position use
end_vertex.makeStartOrEndas seen with the starting waypoint instead ofvertex.addConstraintas you would do for the other waypoints.
Ready, go!
Now we are ready to race! Fire up the virtual race course.
cd ~/vnav-builds/lab4/
./lab4.x86_64
In another terminal, launch tesse_ros_bridge to connect ROS to the simulator,
roslaunch tesse_ros_bridge tesse_quadrotor_bridge.launch
Launch the trajectory follower,
roslaunch trajectory_generation traj_following.launch
And finally, launch the waypoint publisher
roslaunch planner_pkg traj_gen.launch
If everything is working well, your drone should be gracefully going through each gate like this

Note: If the quadcopter flips over after launching the trajectory follower, press r in the Unity window to respwan, the quadcopter should just go back to the starting position.
[Optional] Faster, faster (Extra credit: 15 pts)
How can you make the drone go faster? We will award extra credit to the fastest 3 teams! Current record is 10.3s, achieved by Nikhil Singhal, Fernando Herrera and Chris Chang in 2020.