Exercises

1. Deadline
2. 👤 Individual
   1. 📨 Deliverable 1 - Spy Game [20 pts]
   2. 📨 Deliverable 2 - Well-begun is Half Done [10 pts]
   3. 📨 Deliverable 3 - Feature-based methods for SLAM [10 pts]
   4. 📨 Deliverable 4 [Optional] - Direct methods for SLAM [+5 pts]
   5. 📨 Deliverable 5 [Optional] - From landmark-based SLAM to rotation estimation [+15 pts]

Deadline

This lab (i.e., just a individual portion) will be due on GradeScope on November 6th at 1pm EST.

You should be working on this in conjunction with the team coding portion lab8.5

Note: The team coding portion of this lab will be posted separately as lab9.5, with a separate due date – stay tuned!

👤 Individual

📨 Deliverable 1 - Spy Game [20 pts]

Consider the following spy-style plot of an information matrix (i.e., coefficient matrix in Gauss-Newton’s normal equations) for a landmark-based SLAM problem where dark cells correspond to non-zero blocks:

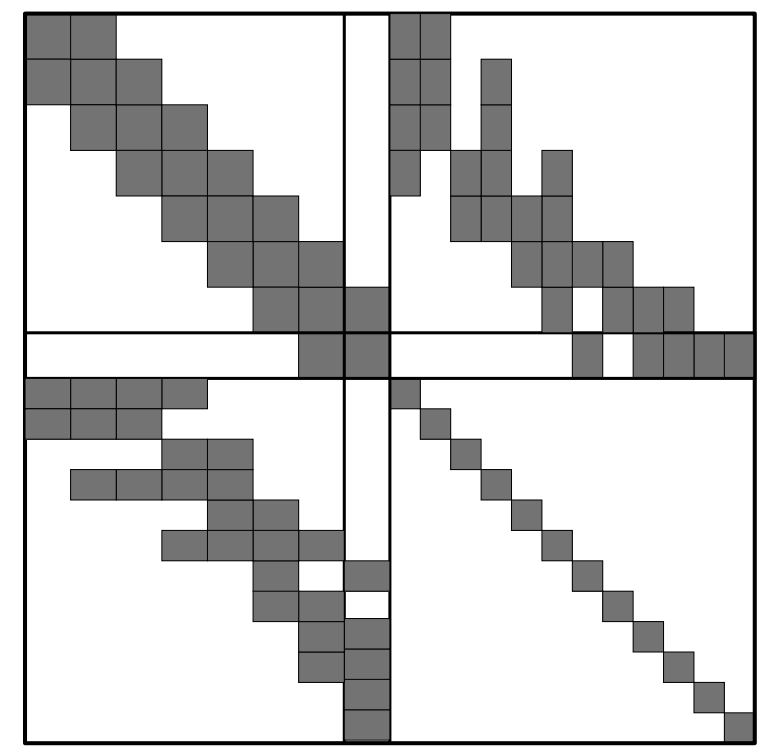
Assuming robot poses are stored sequentially, answer the following questions:

1. How many robot poses exist in this problem?
2. How many landmarks exist in the map?
3. How many landmark have been observed by the current (last) pose?
4. Which pose has observed the most number of landmark?
5. What poses have observed the 2nd landmark?
6. Predict the sparsity pattern of the information matrix after marginalizing out the 2nd feature.
7. Predict the sparsity pattern of the information matrix after marginalizing out past poses (i.e., only retaining the last pose).
8. Marginalizing out which variable (chosen among both poses or landmarks) would preserve the sparsity pattern of the information matrix?
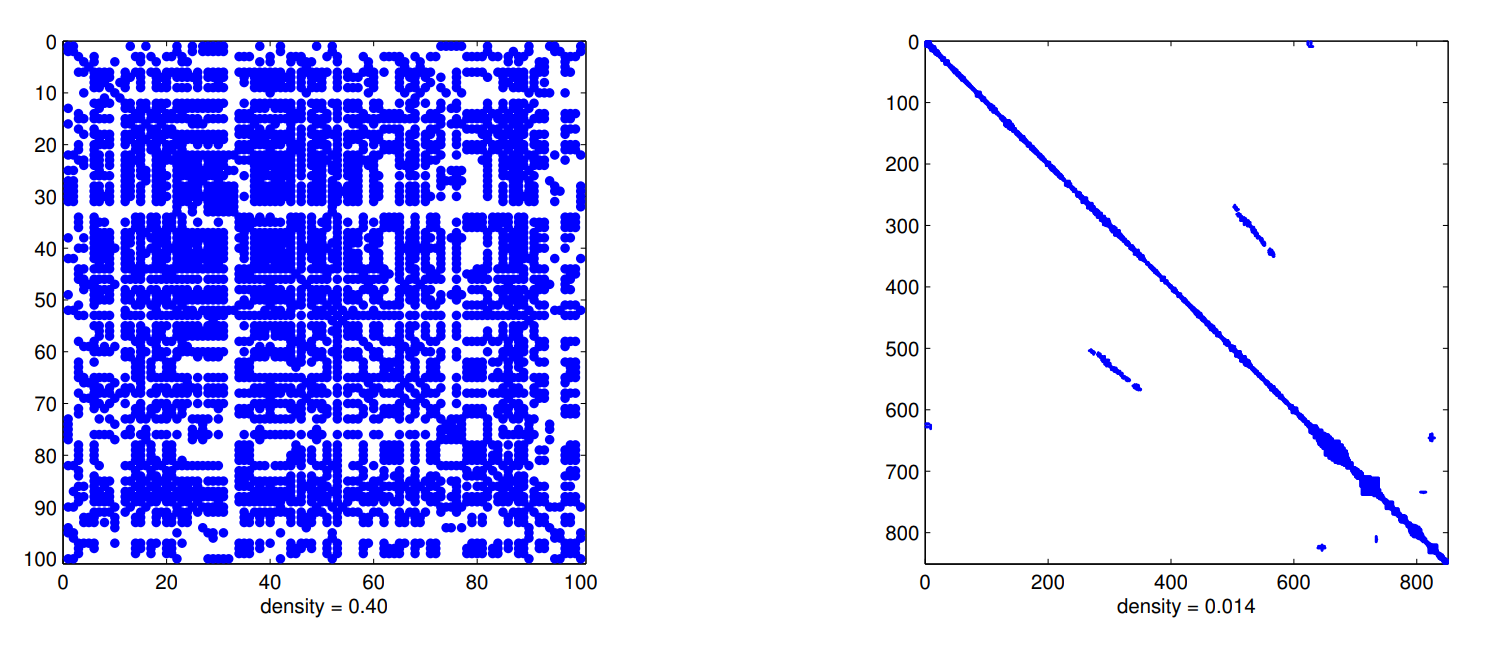
9. The following figures illustrate the robot (poses-poses) block of the information matrix obtained after marginalizing out (eliminating) all landmarks in bundle adjustment in two different datasets. What can you say about these datasets (e.g., was robot exploring a large building? Or perhaps it was surveying a small room? etc) given the spy images below?

📨 Deliverable 2 - Well-begun is Half Done [10 pts]

Pose graph optimization is a non-convex problem. Therefore, iterative solvers require a (good) initial guess to converge to the right solution. Typically, one initializes nonlinear solvers (e.g., Gauss-Newton) from the odometric estimate obtained by setting the first pose to the identity and chaining the odometric measurements in the pose graph.

Considering that chaining more relative pose measurements (either odometry or loop closures) accumulates more noise (and provides worse initialization), propose a more accurate initialization method that also sets the first pose to the identity but chains measurements in the pose graph in a more effective way. A 1-sentence description and rationale for the proposed approach suffices.

Hint: consider a graph with an arbitrary topology. Also, think about the problem as a graph, where you fix the “root” node and initialize each node by chaining the edges from the root to that node..

📨 Deliverable 3 - Feature-based methods for SLAM [10 pts]

Read the ORB-SLAM paper (available here) and answer the following questions:

1. Provide a 1 sentence description of each module used by ORB-SLAM (Fig. 1 in the paper can be a good starting point).
2. Consider the case in which the place recognition module provides an incorrect loop closure. How does ORB-SLAM check that each loop closure is correct? What happens if an incorrect loop closure is included in the pose-graph optimization module?

📨 Deliverable 4 [Optional] - Direct methods for SLAM [+5 pts]

Read the LSD-SLAM paper (available here, see also the introduction below before reading the paper) and answer the following questions:

1. Provide a 1 sentence description of each module used by LSD-SLAM and outline similarities and differences with respect to ORB-SLAM.
2. Which approach (between feature-based or direct) is expected to be more robust to changes in illumination or occlusions? Motivate your answer.

LSD-SLAM is a direct method for SLAM, as opposed to feature-based methods we have worked with previously. As you know, feature-based methods detect and match features (keypoints) in each image and then use 2-view geometry (and possibly bundle adjustment) to estimate the motion of the robot. Direct methods are different in the fact that they do not extract features, but can be easily understood using the material presented in class.

In particular, the main difference is the way the 2-view geometry is solved. In feature-based approaches one uses RANSAC and a minimal solver (e.g., the 5-point method) to infer the motion from feature correspondences. In direct methods, instead, one tries to estimate the relative pose between consecutive frames by minimizing directly the mismatch of the pixel intensities between two images:

\[E(\xi) = \sum_i (I\_{ref}(p_i) - I(\omega (p_i, D\_{ref}(p_i), \xi)))^2 = r_i(\xi)^2\]

Where the objective looks for a pose $\xi$ (between the last frame $I_{ref}$ and the current frame $I$ that minimizes the mismatch between the intensity $I_{ref}(p_i)$ at pixel $p_i$ for each pixel $p_i$ in the image, and intensity of the corresponding pixel in the current image $I$. How do we retrieve the pixel corresponding to $p_i$ in the current image $I$? In other words, what is this term?:

\[I(\omega (p_i, D\_{ref}(p_i), \xi))\]

It seems mysterious, but it’s nothing new: this simply represents a perspective projection. More specifically, given a pixel $p_i$, if we know the corresponding depth $D_{ref}(p_i)$ we can get a 3D point that we can then project to the current camera as a function of the relative pose. The $\omega$ is typically called a warp function since it “warps” a pixel in the previous frame $I_{ref}$ into a pixel at the current frame $I$. What is the catch? Well.. the depth $D_{ref}$ is unknown in practice, so you can only optimize $E(\xi)$ if at a previous step you have some triangulation of the points in the image. In direct methods, therefore these is typically an “initialization step”: you use feature-based methods to estimate the poses of the first few frames and triangulate the corresponding points, and then you can use the optimization of $E(\xi)$ to estimate later poses. The objective function $E(\xi)$ is called the photometric error, which quantifies the difference in the pixel appearance in consecutive frames.

NOTE: LDSO (Direct Sparse Odometry with Loop Closures) which you are going to use in Part 2 of this handout is simply an evolution of LSD-SLAM (by the same authors). We are suggesting you to read the LSD-SLAM paper since it provides a simpler introduction to direct methods, while we decided to use LDSO for the experimental part since it comes with a more recent implementation.

📨 Deliverable 5 [Optional] - From landmark-based SLAM to rotation estimation [+15 pts]

Consider the following landmark-based SLAM problem:

\[\min_{t_i \in \mathbb{R}^3,\ R_i \in \SO{3},\ p_i \in \mathbb{R}^3} \sum_{(i,k) \in \mathcal{E}_l} \| R_i^T(p_k - t_i) - \bar{p}_{ik} \|_2^2 + \sum_{(i,j) \in \mathcal{E}_o} \|R_i^T(t_j - t_i) - \bar{t}_{ij}\|_2^2 + \|R_j - R_i\bar{R}_{ij}\|_F^2\]

Where the goal is to compute the poses of the robot $(t_i, R_i),\ i=1,\ldots,N$ and the positions of point-landmarks $p_k, k= 1, \ldots, M$ given odometric measurements $(\bar{t}_{ij}, \bar{R}_{ij})$ for each odometric edge $(i,j) \in \mathcal{E}_o$ (here $\mathcal{E}_o$ denotes the set of odometric edges), and landmark observations $\bar{p}_{ik}$ of landmark $k$ from pose $i$ for each observation edge $(i,k) \in \mathcal{E}_l$ (here $\mathcal{E}_l$ denotes the set of pose-landmark edges).

• Prove the following claim: “The optimization problem (1) can be rewritten as a nonlinear optimization over the rotations $R_i,\ i=1,\ldots,N$ only.” Provide an expression of the resulting rotation-only problem to support the proof.
  • Hint: i) Euclidean norm is invariant under rotations, and (ii) translations/positions variables appear …! Consider also using a compact matrix notation to rewrite the sums in the cost function otherwise it will be tough to get an expression of the rotation-only problem.
• The elimination of variables discussed at the previous point largely reduces the size of the optimization problem (from 6N+3L variables to 3N variables).However, the rotation problem is not necessarily faster to solve. Discuss what can make the rotation-only problem more computationally-demanding to solve.
  • Hint: What property makes optimization-based SLAM algorithms fast to solve?

---